Финансы » Управление банковскими ресурсами на основе теории нечетких множеств » Нечеткие отношения

Нечеткие отношения

Страница 4

Пример.

Пусть матрица нечеткого отношения R на множестве имеет вид

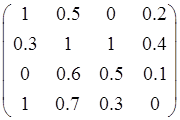
Тогда матрица обычного отношения, являющегося множеством уровня 0,5 этого нечеткого отношения, выглядит так:

.

Операции над нечеткими отношениями.

Перейдем теперь к рассмотрению операций над нечеткими отношениями. Некоторые из этих операций являются аналогами соответствующих операций для обычных отношений, однако, как и в случае нечетких множеств, существуют операции, характерные лишь для нечетких отношений. Заметим, что так же, как и в случае нечетких множеств, операции объединения и пересечения нечетких отношений (и операцию произведения) можно определить различными способами. [4]

Пусть на множестве X заданы два нечетких отношения A и B, т.е. в декартовом произведении заданы два нечетких множества A и B. Нечеткие множества

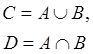
называются соответственно объединением и пересечением нечетких отношений А и В на множестве Х.

Для функции принадлежности получаем

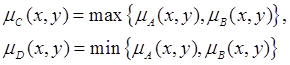
Говорят, что нечеткое отношение В включает в себя нечеткое отношение А, если для нечетких множеств А и В выполнено . Для функций принадлежности этих множеств неравенство выполняется при любых . В рассмотренном выше примере отношений ( ≥ ) и ( >> ) нечеткое отношение содержится в отношении R, т.е. должно быть для любых чисел .

Если R – нечеткое отношение на множестве X, то нечеткое отношение R, характеризующееся функцией принадлежности

,

называется дополнением в Х отношения R.

Дополнение имеет смысл отрицания исходного отношения. Например, для нечеткого отношения R=(лучше) его дополнение R` (не лучше).

Обратное к R нечеткое отношение R-1 на множестве Х определяется следующим образом:

или с помощью функций принадлежности:

.

Важное значение в прикладных задачах имеет произведение или композиция нечетких отношений. В отличие от обычных отношений, произведение нечетких отношений можно определить различными способами. Здесь мы приведем некоторые из возможных определений этой операции. [3]

Определение 3.11.

Максиминное произведение нечетких отношений А и В на множестве Х характеризуется функцией принадлежности вида

.

В случае конечного множества Х матрица нечеткого отношения равна максиминному произведению матриц отношений А и В, т.е. получается с помощью тех же операций, что и матрица произведения обычных отношений.

Определение 3.11а.

Минимаксное произведение нечетких отношений А и В на Х определяется функцией принадлежности вида

Определение 3.11б.

Максимультипликативное произведение нечетких отношений А и В определяется функцией принадлежности

Для сравнения друг с другом введенных операций произведения приведем простой пример произведения отношений А и В на конечном множестве X, состоящем из двух элементов.

Популярные материалы:

Банковская система России: тенденции развития
В современной экономике главенствующую функцию по формированию денежной массы, ее предложению экономиче­ским структурам, оценке покупательной способности отдель­ных экономических агентов выполняют банковские системы. Банковская система — это совокупность разных взаимосвя­занных банков и других кред ...

Рекомендации по повышению кредитоспособности ООО «Транскомплект»
Задачи, направленные на корректировку финансовой политики предприятия, ставятся руководством (менеджерами, собственниками). В этом случае можно сказать, что результаты финансового анализа предназначены для внутренних пользователей; они должны помочь определить наиболее эффективные пути улучшения (с ...

Оценка величины капитала коммерческого банка
Для того чтобы банковское регулирование было теснее связано с величиной банковского капитала, банки следует отнесены к одной из пяти групп, в зависимости от величины их банковского капитала. Меньшая величина банковского капитала - жестче регулирование. От банков с недостаточной величиной капитала о ...